Advent of Code 2023, Day 14

December 14, 2023 7 minute read

❄️ Back to Advent of Code 2023 solutions homepage ❄️

# Imports
from aoc23.utils import read_input

input_14 = read_input(14)

Part 1

In part 1 of this puzzle, we are given a large array containing 3 types of characters, representing different physical objects sitting on top a moveable platform:

O = round rocks, which roll when the platform is tilted
# = cubic rocks, which do not move when the platform is tilted
. = empty space.

Here are the first few rows of the array to illustrate:

input_14[:5]

['O...#.O.OOO.OO.O.OOO...........OO#..##...#...#.O.#.O....#.##..#.#.OOO.O....#....O...O..OOOO.O#......',
 'O#OO....#O....O..#..###....#.#..#.......#..#.#....O...O.#..O.O#.....#.O#...O.O..##..OO.#...O.O#.....',
 '.O...#..#...##....##....O.OO#O....O.O..#O.....#O.O....#.#O#.#O......#O.....#.O..O.....O.....O...O##.',
 '..O...#OO..O....OO.....OOOO#O.OO..#.........O.O........O..#.........##...O.........O#..O.....#O.OO##',
 'OO.O....#O#..O..#.OO....OO.#.OO...##.O..O..O....OO...O....#.....#..O#OO....#....O.....OO.#.O......OO']

When the platform is tilted, the round rocks roll in the direction of the tilt, until they hit either a cubic rock or the edge of the array. The first task is to find the new arrangement after the platform has been tilted to the north (the top edge of the array).

In anticipation of being asked later to tilt the platform in other directions too, let’s consider an effective way of handling all the cardinal directions. It is possible to reduce tilts in all 4 cardinal directions into tilts in just one direction, by transforming the array before applying the tilt, and then transforming back. The most natural direction to start with is west-east (as this is the direction in which the row strings span), so pick east as the default direction - this is convenient, is when a string of O and # characters is sorted, the Os end up on the eastern side. Here is how tilts in other directions can be converted into tilts in the east direction:

West: flip the array in the east-west direction, apply the tilt to the east, and then flip back
South: transpose the array, apply the tilt to the east, and transpose back
North: flip the array in the north-south direction, transpose, apply the tilt to the east, transpose and flip back.

The strategy for tilting in the east direction is simple - for each row string:

Split on the # characters
Sort each intermediate string, to push the Os to the eastern edge
Join back together with connecting # characters.

def roll_east(grid: list[str]) -> list[str]:
    return [
        '#'.join([''.join(sorted(round_rocks)) for round_rocks in row.split('#')]) 
        for row in grid
    ]
        

roll_east(['##OO.O...#..O..#'])

['##....OOO#....O#']

As described above, the general roll_direction function makes use of the roll_east function and the helper transpose function:

def transpose(grid: list[str]) -> list[str]:
    return list(map(lambda x: ''.join(x), zip(*grid)))

def roll_direction(grid: list[str], direction: str) -> list[str]:
    match direction.lower():
        case 'n':
            # Flip -> transpose -> tilt east -> transpose -> flip
            flipped_grid = transpose(grid[::-1])
            rolled_grid = roll_east(flipped_grid)
            return transpose(rolled_grid)[::-1]
        
        case 'e':
            return roll_east(grid)
        
        case 's':
            # Transpose -> tilt east -> transpose
            flipped_grid = transpose(grid)
            rolled_grid = roll_east(flipped_grid)
            return transpose(rolled_grid)
        
        case 'w':
            # Flip -> tilt east -> flip
            flipped_grid = [row[::-1] for row in grid]
            rolled_grid = roll_east(flipped_grid)
            return [row[::-1] for row in rolled_grid]
        
        case _:
            raise ValueError('Direction not recognised!')
    

To test this, take advantage of the provided test grid:

test_grid = [
    'O....#....',
    'O.OO#....#',
    '.....##...',
    'OO.#O....O',
    '.O.....O#.',
    'O.#..O.#.#',
    '..O..#O..O',
    '.......O..',
    '#....###..',
    '#OO..#....'
]

print(f'    N                E                S                W')
for row_N, row_E, row_S, row_W in zip(roll_direction(test_grid, 'n'), 
                                      roll_direction(test_grid, 'e'),
                                      roll_direction(test_grid, 's'),
                                      roll_direction(test_grid, 'w')):
    print(f'{row_N}       {row_E}       {row_S}       {row_W}')

    N                E                S                W
OOOO.#.O..       ....O#....       .....#....       O....#....
OO..#....#       .OOO#....#       ....#....#       OOO.#....#
OO..O##..O       .....##...       ...O.##...       .....##...
O..#.OO...       .OO#....OO       ...#......       OO.#OO....
........#.       ......OO#.       O.O....O#O       OO......#.
..#....#.#       .O#...O#.#       O.#..O.#.#       O.#O...#.#
..O..#.O.O       ....O#..OO       O....#....       O....#OO..
..O.......       .........O       OO....OO..       O.........
#....###..       #....###..       #OO..###..       #....###..
#....#....       #..OO#....       #OO.O#...O       #OO..#....

Looking good to me! To complete the first part of the puzzle, the load on the top edge of the grid should be computed - each round rock provides a contribution equal to the number of rows that lie further to the south than it (including the row it is on):

def compute_load(grid: list[str]) -> int:
    n_rows = len(grid)
    
    load = 0    
    for i, row in enumerate(grid):
        # Number of rocks in row
        n_rocks = sum([char == 'O' for char in row])
        
        # Load contribution from row
        load += n_rocks*(n_rows - i)
        
    return load

The test grid provides one further check of the load logic:

assert compute_load(roll_direction(test_grid, 'n')) == 136
print('Success!')

Success!

Applying this to the full input array gives the total load:

compute_load(roll_direction(input_14, 'n'))

So the answer to part 1 is: 109596.

Part 2

As anticipated, in the second part we are asked to consider a more complex operation on the grid called a spin cycle - this consists of all four tilts in sequence, in the order (N, W, S, E).

def spin_cycle(grid: list[str]) -> list[str]:
    grid = roll_direction(grid, 'n')
    grid = roll_direction(grid, 'w')
    grid = roll_direction(grid, 's')
    grid = roll_direction(grid, 'e')
    
    return grid

The puzzle asks us to consider applying the spin_cycle operation $N=1000000000$ times; the timeit test below estimates that it takes (using my unoptimised code) about 87 µs to perform a spin cycle. Therefore, this many operations would take 87,000 seconds, or more than a whole day - clearly, there is a smarter way to find the $N$th iteration of the grid.

%timeit spin_cycle(test_grid)

85.7 µs ± 2.68 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

Intuitively, it makes sense that after a certain number of applications of spin_cycle (certainly less than $N=1000000000$), the round rocks will return to a state already previously seen. After all, there are only so many ways in which the rocks can be arranged among the fixed rocks, particularly considering each tilt operation pushes the round rocks as far as possible towards each edge. As the result of each spin cycle is completely determined by the starting grid, once a previously visited arrangement is found, the spin cycles will loop around the subsequent states with a certain cycle length.

Making the assumption that this point will be found by considerably fewer iterations, the strategy becomes:

Apply spin_cycle to the grid, and make a note of the state the the grid ends up in (as well as the position in the chain)
Repeat until a previously visited grid state is seen
Compute the cycle length, and the number of states before the hitting first state in the cycle.

This is reminiscent of the puzzle from day 8, and we can create a similar diagram to visualise what is going on:


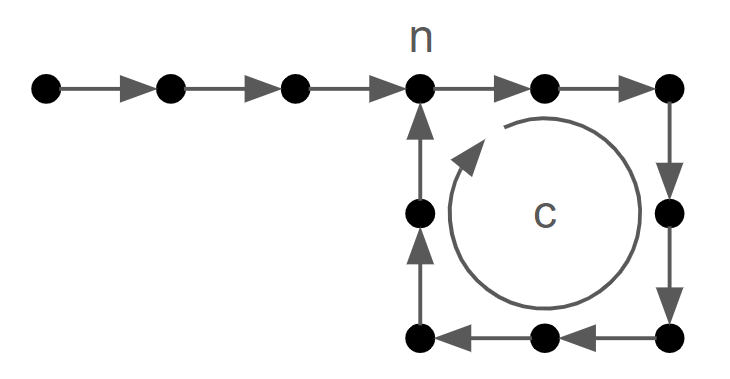It takes $n$ steps to reach the first grid state in the cycle, and the cycle is of length $c$.

Once the numbers $n$ and $c$ are found, consider expressing the total number of iterations $N$ as:

\[N = n + kc + r\]

where $k\in\mathbb{N}$ and $r<c$. As the state is unchanged after going around the loop an integer number of times, the final state is the same as the state found after iterating a smaller number of times:

\[\hat{N} = n + r.\]

Now, implementing this to find the final grid state:

def spin_cycle_n_times(input_grid: list[str], N: int) -> list[str]:
    # Initialise to keep track of found grids
    grid = input_grid
    found_grids = {''.join(grid): 0}
    
    # Loop up to N (max possible value needed)
    for i in range(N):
        grid = spin_cycle(grid)
        grid_str = ''.join(grid) # hashable
        
        if grid_str in found_grids:
            # Already found grid - compute n and c
            # and stop iterating
            n_plus_c = i+1
            n = found_grids[grid_str]
            c = n_plus_c - n
            break
        
        else:
            # Add new grid to dictionary
            found_grids[grid_str] = i + 1
    else:
        # return final grid, if no previously 
        # found grid observed
        return grid
    
    # remainder and new N
    print(f'n = {n}, c = {c}')
    r = (N - n) % c
    N_hat = n + r
    
    # Invert grid
    final_grid = [k for k, v in found_grids.items() if v == N_hat][0]

    # Convert grid_str back into grid
    m, n = len(input_grid), len(input_grid[0])
    return [final_grid[n*i:n*(i+1)] for i in range(m)]

Helpfully, the puzzle provides the value of the the load when the test grid is spin cycled $N$ times as a test of this function:

N = 1_000_000_000
compute_load(spin_cycle_n_times(test_grid, N))

n = 3, c = 7

64

Also, we see that only 10 versions of the original/spin-cycled grid were needed in order to find all possible future spin-cycled versions. Repeating this for the full input array:

compute_load(spin_cycle_n_times(input_14, N))

n = 96, c = 11

96105

Similarly, only 107 versions of the grid were necessary here to find all possible future spin-cycled versions - a significant reduction.

Michael Cole

Advent of Code 2023, Day 14

Part 1

Part 2

Share on

Comments

You May Also Enjoy

How to play one player 501

How can I reach checkout before my opponent?

How do I throw high scoring darts?

The Quadro board - why did it flop?