Advent of Code 2023, Day 8

❄️ Back to Advent of Code 2023 solutions homepage ❄️

# Imports
from aoc23.utils import read_input
import math

input_8 = read_input(8)

Part 1

In today’s puzzle, we are considering a collection of nodes labelled by three-letter codes (from $AAA$ to $ZZZ$), and maps describing how these nodes are connected. From each node, a left (‘L’) or right (‘R’) turn maps to a new node, determined by the puzzle input. Also provided is a list of instructions to follow at each step, consisting of a sequence of ‘L’ and ‘R’ characters.

First, extract the instructions and the maps from the input file:

instructions = input_8[0]
map_lines = input_8[2:]

maps = {}
for line in map_lines:
    s = line.split()
    k = s[0]
    v = {'L': s[2][1:-1], 'R': s[3][:-1]}
    maps[k] = v
maps['AAA']

{'L': 'DCX', 'R': 'FDP'}

We are asked to find the number of steps, when following the instructions (and repeating them from the start if exhausted), starting from the node ‘AAA’:

node = 'AAA'
steps = 0
while node != 'ZZZ':
    for instr in instructions:
        steps += 1
        node = maps[node][instr]
        if node == 'ZZZ':
            break

steps

16579

So the answer to part 1 is: 16579.

Part 2

In the second part, we need to track not just the $AAA$ node, but also all the other nodes ending in ‘A’, of which there are 6:

start_nodes = [node for node in maps if node[2] == 'A']

start_nodes

['KTA', 'PLA', 'LJA', 'AAA', 'JXA', 'NFA']

To formalize the setup a bit more, let’s define the following quantities:

• The starting nodes ${A_i}$ for $1\le i\le 6$
• The ‘state’ of each chain is given by $(N_i, j)$, where $N_i$ is the current node, and $j$ is the index of the instruction which is about to be followed. The path from each state $(N_i, j)$ is uniquely determined by the instruction set and the node maps, and is the same each time the state is revisited.
• At some point, the chain will return to a previously visited state - this is guaranteed, as there are only finitely many (node, instruction) pairs. Once this happens, the chain will loop around indefinitely, with cycle length $C_i$.
• For each starting node $A_i$, the numbers of steps taken before a destination state is reached for the first time is $Z_i=(t^{(i)}_1, t^{(i)}_2, …)$, with $t^{(i)}_1<t^{(i)}_2<…$ Once the cycle starts repeating, we can stop recording these, as any number of steps of the form $t^{(i)}_1+kC_i$ will also be a valid entry; in this way the collection of steps $Z_i$ remains finite.

The behaviour of each chain can be visualized in the diagram below. Each node in the diagram represents a state of the chain; for example, for one of the chains, the first node $A$ is $(AAA, 0)$ and the node $Z$ is $(ZZZ, k)$ for some instruction index $k$.

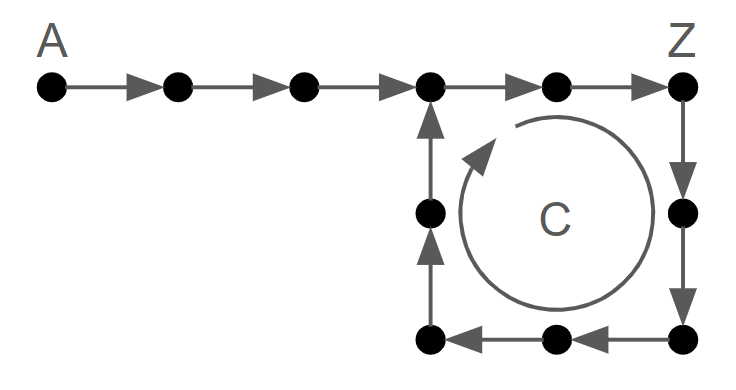It takes $Z$ steps to reach the destination nodes, and the cycle is of length $C$.

With these definitions, let’s now investigate the chains originating from each of the 6 starting nodes. First, define a function that will calculate the list of visited states from a starting node:

def compute_visited(start_node, instructions, maps):
    # Computes the list of (node, instruction_index) states, starting from start_node, 
    # as well as the the first repeated element of the list (defining the start 
    # of the cycle)
    visited = []
    state = (start_node, 0)
    instruction_idx = 0
    while state not in visited:
        visited.append(state)
        instruction_idx = (instruction_idx + 1) % len(instructions)
        state = (maps[state[0]][instructions[state[1]]], instruction_idx)
    return visited, state

Also, adapt the code from earlier, computing the number of steps needed to reach the first destination node (ending ‘Z’):

def num_steps(node, instructions, maps):
    # Computes the number of steps taken to reach the first destination node
    steps = 0
    while node[2] != 'Z':
        for instr in instructions:
            steps += 1
            node = maps[node][instr]
            if node[2] == 'Z':
                break
    return steps

Now, compute for each of the chains:

• The list of visited states
• The first repeated node (the start of the cycle repeating)
• The length of the cycle, once it starts repeating ($C_i$)
• The number of steps taken to reach destination states for the first time ($Z_i$)

visited = {}
next_nodes = {}
cycle_lengths = {}
Z = {}
for start_node in start_nodes:
    vis, k = compute_visited(start_node, instructions, maps)
    visited[start_node] = vis
    next_nodes[start_node] = k
    cycle_lengths[start_node] = len(vis) - vis.index(k)
    Z[start_node] = num_steps(start_node, instructions, maps)

The first question to ask is: do the visited paths of two different start nodes intersect? If they do, then the same initial node may lead into the same cycle, and the chains could potentially never finish on a destination node simultaneously. The visited lists can be intersected, to see if there is any overlap:

matches = []
for n1 in start_nodes:
    for n2 in start_nodes:
        if n1 == n2:
            continue
        intersection = set(visited[n1]).intersection(set(visited[n2]))
        if len(intersection) > 0:
            matches.append((n1, n2))
matches

[]

There are no matches - so the chains for each starting node are distinct and non-overlapping. As there are only 6 destination nodes, there must be one in each of these chains (otherwise the problem is impossible!). Another further thing to consider is how many times a destination state (of the form $(XXZ, k)$ for some destination node $XXZ$ and some index $k$) appears in each visited state list:

[[state for state in visited[start_node] if state[0][2] == 'Z'] for start_node in start_nodes]

[[('DLZ', 0)],
 [('RGZ', 0)],
 [('BGZ', 0)],
 [('ZZZ', 0)],
 [('NTZ', 0)],
 [('HBZ', 0)]]

Luckily for us, there is a unique destination state in each of the chains! Given all this information, we can set up the problem as a set of linear congruence relations. Let $N$ be the smallest number of steps taken, until all destination nodes are visited simultaneously. Considering the $i$th chain, $N$ must be of the form:

\[N = Z_i + kC_i\]

for some $k\in\mathbb{N}_0$. Combining these relations for all the chains gives the set of simultaneous congruence relations:

\[N \equiv Z_1 \:\text{mod}\; C_1 \\ N \equiv Z_2 \:\text{mod}\; C_2 \\ N \equiv Z_3 \:\text{mod}\; C_3 \\ N \equiv Z_4 \:\text{mod}\; C_4 \\ N \equiv Z_5 \:\text{mod}\; C_5 \\ N \equiv Z_6 \:\text{mod}\; C_6\]

where the $Z_i$ have been reduced modulo $C_i$. For the general case, the Chinese Remainder Theorem may be used to find the smallest $N$ that satisfies this set of congruences. Fortunately, the task is made easier by the following observation:

for start_node in start_nodes:
    print(f'Start node = {start_node}, Z_i = {Z[start_node]}, C_i = {cycle_lengths[start_node]}')

Start node = KTA, Z_i = 14893, C_i = 14893
Start node = PLA, Z_i = 19951, C_i = 19951
Start node = LJA, Z_i = 22199, C_i = 22199
Start node = AAA, Z_i = 16579, C_i = 16579
Start node = JXA, Z_i = 17141, C_i = 17141
Start node = NFA, Z_i = 12083, C_i = 12083

Each of the remainders is $\equiv 0$ when reduced modulo $C_i$; in this special case, the solution $N$ is just the lowest common multiple of the cycle lengths $C_i$:

math.lcm(*cycle_lengths.values())

So the answer to part 2 is: 12927600769609.

Further reading:

• Chinese remainder theorem - the general method to use when faced with a set of simultaneous linear congruences

❄️ Back to Advent of Code 2023 solutions homepage ❄️