Advent of Code 2023, Day 3
❄️ Back to Advent of Code 2023 solutions homepage ❄️
# Imports
from aoc23.utils import read_input
import math
from collections import defaultdict
input_3 = read_input(3)
Part 1
input_3[0]
'................458...689.556..3............197......582........720.........................515..352..286.........670.741.....895.626.......'
line_length = len(input_3[0])
To start, let’s pad each the input by adding a line of . characters at the start and end of the input. By doing this, we won’t need to worry about handling the start and end lines differently, as long as we remember to start at the second line and end at the penultimate line:
padded_input = [line_length*'.', *input_3, line_length*'.']
Also, adding an extra . to the start and end of each line will not change the result, but will mean we can treat each character of the original string equally (i.e. no special treatment for the first or last character):
padded_input = [f'.{line}.' for line in padded_input]
padded_input_trimmed = [line[:100] for line in padded_input]
We end up with a padded input that looks like this:
for line in padded_input[:5]:
print(line)
..............................................................................................................................................
.................458...689.556..3............197......582........720.........................515..352..286.........670.741.....895.626........
....910.743..........................13..........................*.............775...956........@.........*................971.-..............
.....*......406.507.97..846..............968+.........253........730...574............#....308......*.....798..............*.......894........
.....555...............*......%...............980.+43..=..239..........*......495................638.111.........*490...124...*........576....
Now, let’s create some helper functions which will be useful for the main function later on:
def is_symbol(char: str) -> bool:
return (not char.isalnum()) and (char != '.')
def current_number_list_to_int(current_number_list: list[str]) -> int:
return int(''.join(current_number_list))
The strategy for finding all the ‘part-numbers’ (the numbers which are adjacent to a symbol) is the following:
Create a size (len(lines), len(line[0]) array, where each element is a boolean
indicating whether the corresponding character from the grid is a symbol or not.
For each line (excluding first and last):
For each character in the string:
If the character is a number:
Check if the characters above/below and to the left are symbols
If so, update the number inclusion flag
If the character is a symbol, or the character above/below or above/below and to the left is a symbol:
Update the number inclusion flag
If we have reached the end of a number and the number inclusion flag is True:
Append the number to the inclusion list
If the character is a '.':
Turn the number inclusion flag off
This diagram might help visualise the elements of the boolean symbol array which are being checked at each step:
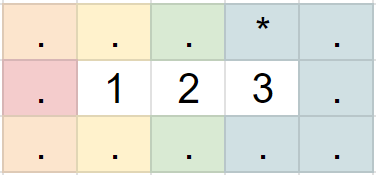 |
|---|
| The order in which the elements of the symbol array are checked, as we loop over centre line |
| (red -> orange -> yellow -> green -> blue) |
def part_numbers(lines: list[str]) -> list[int]:
integer_list = []
line_length = len(lines[0])
symbol_arr = [[is_symbol(i) for i in line] for line in lines]
for i in range(1, len(lines)-1):
# Initialise quantities for this line
line = lines[i]
add_this_number = False
current_number_list = []
for j in range(line_length):
# If this character is a digit, check for symbols above and below
if line[j].isdigit():
add_this_number = any([add_this_number,
symbol_arr[i-1][j-1],
symbol_arr[i+1][j-1]])
current_number_list.append(line[j])
else:
if symbol_arr[i][j] or symbol_arr[i-1][j] or symbol_arr[i+1][j] or symbol_arr[i-1][j-1] or symbol_arr[i+1][j-1]:
# Update flag if in neighbourhood of symbol
add_this_number = True
if add_this_number and len(current_number_list) > 0:
# Update inclusion list if flag is True
integer_list.append(current_number_list_to_int(current_number_list))
current_number_list = []
if line[j] == '.':
# Reset flag
add_this_number = False
current_number_list = []
return integer_list
sum(part_numbers(padded_input))
531561
Part 1 answer: 531561.
This puzzle was quite fiddly, so I wrote some quick example cases which can be used to check if the code is working as intended:
test_inputs = [
['.....',
'..1..',
'.....'],
['.*...',
'..1..',
'.....'],
['..*..',
'..1..',
'.....'],
['...*.',
'..1..',
'.....'],
['.....',
'..1*.',
'.....'],
['.....',
'..1..',
'...*.'],
['.....',
'..1..',
'..*..'],
['.....',
'..1..',
'.*...'],
['.....',
'.*1..',
'.....']
]
test_answers = [[], [1], [1], [1], [1], [1], [1], [1], [1]]
for test_input, test_answer in zip(test_inputs, test_answers):
assert part_numbers(test_input) == test_answer, f"{test_input}"
print('All passed!')
All passed!
Part 2
def compute_gear_numbers(lines):
gear_list = []
line_length = len(lines[0])
gear_arr = [[i=='*' for i in line] for line in lines]
for i in range(1, len(lines)-1):
# Initialise quantities for this line
line = lines[i]
add_this_number = False
current_number_list = []
current_gear_locations = []
for j in range(line_length):
# If this character is a digit, check for gears above and below
if line[j].isdigit():
add_this_number = any([add_this_number,
gear_arr[i-1][j-1],
gear_arr[i+1][j-1]])
if gear_arr[i-1][j-1]:
current_gear_locations.append((i-1, j-1))
if gear_arr[i+1][j-1]:
current_gear_locations.append((i+1, j-1))
current_number_list.append(line[j])
else:
for m, n in [(i, j), (i-1, j), (i+1, j), (i-1, j-1), (i+1, j-1)]:
if gear_arr[m][n]:
add_this_number = True
current_gear_locations.append((m, n))
if add_this_number and len(current_number_list) > 0:
gear_list.append([current_number_list_to_int(current_number_list), set(current_gear_locations)])
current_number_list = []
if line[j] == '.':
add_this_number = False
current_number_list = []
current_gear_locations = []
return gear_list
gear_numbers = compute_gear_numbers(padded_input)
gear_numbers[:5]
[[720, {(2, 65)}],
[286, {(2, 106)}],
[910, {(3, 5)}],
[971, {(3, 123)}],
[846, {(4, 23)}]]
For each number, we now have a set of locations of the neighbouring * characters. We can invert this, to create a map from * locations to neighbouring numbers:
d = defaultdict(list)
for number, gear_locations in gear_numbers:
for gear_location in gear_locations:
d[gear_location].append(number)
And finally, by summing up the products of the numbers which are neighbouring the same *, we get our final answer:
sum_ratios = 0
for gear_location, numbers in d.items():
assert len(numbers) <= 2, "Don't know how to handle 3 or more numbers next to same gear!"
if len(numbers) == 2:
sum_ratios += math.prod(numbers)
sum_ratios
83279367
Part 2 answer is: 83279367.



Comments