Advent of Code 2023, Day 25

❄️ Back to Advent of Code 2023 solutions homepage ❄️

# Imports
from aoc23.utils import read_input
import networkx as nx
import numpy as np

input_25 = read_input(25)

Part 1

The Christmas Day puzzle is here! We are given an adjacency list for a large number of nodes, describing the ways in which the nodes are connected together by wires. This defines a graph, which we are told has a minimum cut with only three crossing edges (these represent 3 wires that, when cut, divide the nodes into two unconnected components). Let’s start by using the networkx graph manipulation package to convert the example adjacency list and the full adjacency list into networkx.Graph objects:

def process_input(input_list):
    g = nx.Graph()
    
    # Define and add all the edges from each line
    for line in input_list:
        node1, conns = line.split(': ')
        for conn in conns.split():
            g.add_edge(node1, conn, name=f'{node1} -> {conn}')
            
    return g

test_input = [
    'jqt: rhn xhk nvd',
    'rsh: frs pzl lsr',
    'xhk: hfx',
    'cmg: qnr nvd lhk bvb',
    'rhn: xhk bvb hfx',
    'bvb: xhk hfx',
    'pzl: lsr hfx nvd',
    'qnr: nvd',
    'ntq: jqt hfx bvb xhk',
    'nvd: lhk',
    'lsr: lhk',
    'rzs: qnr cmg lsr rsh',
    'frs: qnr lhk lsr'
]

test_graph = process_input(test_input)
graph = process_input(input_25)

As this is Christmas Day, we can try to avoid some work by seeing if there is an easy way to spot the min-cut edges with a visualization:

nx.draw(graph, with_labels=True,
        pos=nx.spring_layout(graph, weight=None, iterations=200))

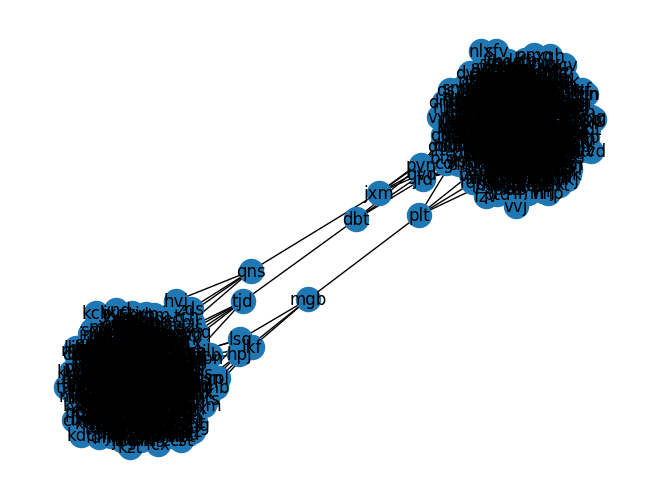Visualization of the connected graph - the three min-cut edges are clearly visible

Fortunately, we can see the three edges connecting the two clusters quite clearly! By inspection, reading off the node names and removing the associated edges:

graph.remove_edge('tjd', 'dbt')
graph.remove_edge('jxm', 'qns')
graph.remove_edge('plt', 'mgb')

And just to check, re-visualize the graph to see if the nodes are now partitioned into unconnected clusters:

nx.draw(graph, with_labels=True,
        pos=nx.spring_layout(graph, weight=None, iterations=200))

Visualization of the cut graph - now disconnected into two parts

Great! networkx has a method called connected_components which will determines the sizes of each of these clusters:

conn = nx.connected_components(graph)
sizes = [len(c) for c in conn]
print(f'Connected component sizes: {sizes}')

Connected component sizes: [752, 730]

np.prod(sizes)

548960

So the answer to part 1 is: 548960.

We were fortunate in this case that visualization the graph was sufficient to find the three min-cut edges - if this were not the case, there is a method called the Stoer Wagner algorithm which finds the minimum-cut in polynomial time (in the number of vertices); luckily, the networkx package has this available out of the box:

test_cut_value, test_partition = nx.stoer_wagner(test_graph)

assert test_cut_value == 3
test_partition

(['lhk', 'cmg', 'rsh', 'rzs', 'pzl', 'frs', 'lsr', 'qnr', 'nvd'],
 ['bvb', 'ntq', 'hfx', 'xhk', 'rhn', 'jqt'])

This matches exactly what was expected for the provided example - let’s repeat for the full graph (first, re-ininitialise so it has the full set of edges):

graph = process_input(input_25)
cut_value, partition = nx.stoer_wagner(graph)

Now, we should be able to reproduce the correct partition component sizes, and the final answer:

assert cut_value == 3
np.prod([len(p) for p in partition])

548960

Part 2

The second part of this puzzle only asks us to provide all 49 stars from the first 24 days, plus part 1 from today - this gives us the final star, and completes the Advent of Code 2023!

Advent of Code 2023 complete!

❄️ Back to Advent of Code 2023 solutions homepage ❄️