Advent of Code 2023, Day 20

December 20, 2023 13 minute read

❄️ Back to Advent of Code 2023 solutions homepage ❄️

# Imports
from aoc23.utils import read_input
import math
from dataclasses import dataclass
from abc import abstractmethod, ABC
from collections import deque

input_20 = read_input(20)

Part 1

In the first part of today’s puzzle, we are given details of a collection of communication modules, which are able to send high and low pulses to each other. Each module is one of a number of different types, each with a different behaviour:

Flip-flop module: defaults to Off, and has the following behaviour when receiving a pulse:

Setting	High pulse	Low pulse
On	Nothing	Turn off, send low pulse
Off	Nothing	Turn on , send high pulse

Conjunction module: defaults to remembering low pulse from each input, and then after receiving a new pulse and updating its memory:

Memory	Receive pulse
High for all inputs	Send low pulse
Low for at least one input	Send high pulse

Broadcaster module:

High pulse	Low pulse
Send high pulse	Send low pulse

Let’s create some classes which will represent each of the communcation modules, and handle the receiving and transmission of pulses. Each will be an example of a Module, which provides the abstract base class for all the other modules:

class Module(ABC):
    
    def __init__(self, connected):
        self.connected = connected
        super().__init__()
    
    @abstractmethod
    def process_pulse(self, pulse):
        raise NotImplementedError()
        
    @abstractmethod
    def reset(self):
        raise NotImplementedError()

The following dataclass will track each pulse, remembering the pulse type (low or high) as well as the source and target modules for the pulse:

@dataclass
class Pulse:
    pulse_type: str
    origin: Module
    destination: Module
        
    def __repr__(self):
        return f'{self.origin} -{self.pulse_type}-> {self.destination}'

First, the flip-flop module:

class FlipFlop(Module):
    
    def __init__(self, name, connected):
        super().__init__(connected)
        self.name = name
        self.state = False
        
    def __repr__(self):
        return f'flipflop_{self.name}'
    
    def process_pulse(self, pulse):
        # Check that pulse is coming to this module
        assert pulse.destination == self.name
        
        # Do nothing if high pulse
        if pulse.pulse_type == 'high':
            return []
        
        # If low pulse, send low/high pulse
        # and flip module state
        elif pulse.pulse_type == 'low':
            pulses = [
                Pulse(pulse_type='low' if self.state else 'high',
                      origin=self.name,
                      destination=module)
                for module in self.connected
            ]
            self.state = not self.state
            return pulses
        
    def reset(self):
        self.state = False

Next, the Conjunction module, which has a memory of the pulses from each input module stored as a dict. This is initially empty, so when an instance of Conjunction is created, this memory needs to be populated with low values for any module that has the potential to send a pulse to it.

class Conjunction(Module):
    
    def __init__(self, name, connected):
        super().__init__(connected)
        self.name = name
        
        # Initially empty - needs to be
        # populated on initialization!
        self.states = {}
        
    def __repr__(self):
        return f'conj_{self.name}'
    
    def process_pulse(self, pulse):
        # Check that pulse is coming to this module
        assert pulse.destination == self.name
        
        # Update module memory
        origin = pulse.origin
        self.states[origin] = pulse.pulse_type
        
        # Sent pulse depends on memory of all inputs
        if all([pulse_type == 'high' for pulse_type in self.states.values()]):
            out_pulse_type = 'low'
        else:
            out_pulse_type = 'high'
            
        # Send pulses to all connected modules
        return [
            Pulse(pulse_type=out_pulse_type,
                  origin=self.name,
                  destination=module)
                for module in self.connected
        ]
    
    def reset(self):
        self.states = {state: 'low' for state in self.states}

The Broadcaster module transmits any input pulse to all of the connected output modules:

class Broadcaster(Module):
    
    def __init__(self, name, connected):
        super().__init__(connected)
        self.name = name
        
    def __repr__(self):
        return f'{self.name}'
    
    def process_pulse(self, pulse):
        # Broadcast pusle to all connected modules
        return [
            Pulse(
                pulse_type=pulse.pulse_type,
                origin=self.name,
                destination=module)
            for module in self.connected
        ]
    
    def reset(self):
        pass

Finally, any module not recognised as a flip-flop, conjunction or broadcaster is classed as an UntypedModule, which can receive pulses but never transmits any:

class UntypedModule(Module):
    
    def __init__(self, name, connected):
        super().__init__(connected)
        self.name = name
        
    def __repr__(self):
        return f'{self.name}'
    
    def process_pulse(self, pulse):
        # No pulses transmitted
        return []
    
    def reset(self):
        pass

For each row in the input file, the first character(s) determines the type of module (% = flip-flop, # = conjunction, broadcaster = broadcaster, anything else = untyped). So loop over all of the rows, creating a Module object of some kind for each of them. There may also be modules which do not have their own rows, but are defined in the connected modules of another row - this needs to be checked after the first pass over the rows, and while doing this the states for all the Conjunction modules can also be properly initialised.

def process_input(input_lines):
    modules = {}
    
    for line in input_lines:
        module_string, conn_string = line.split(' -> ')
        connected = conn_string.split(', ')
        # Flip-flops
        if module_string[0] == '%':
            name = module_string[1:]
            modules[name] = FlipFlop(name, connected)
            
        # Conjunctions
        elif module_string[0] == '&':
            name = module_string[1:]
            modules[name] = Conjunction(name, connected)
            
        # Broadcasters
        elif module_string == 'broadcaster':
            modules['broadcaster'] = Broadcaster('broadcaster', connected)
            
        # Untyped
        else:
            modules[module_string] = UntypedModule(module_string, connected)
    
    # Check for any uninitialised modules
    # and in the meantime initialise the
    # states for Conjunction modules
    unfound_modules = {}
    for module_name, module in modules.items():
        for out in module.connected:
            
            if out not in modules:
                # Uninitialised module
                unfound_modules[out] = UntypedModule(out, [])
                
            elif isinstance(modules[out], Conjunction):
                # Conjunction module - add to state
                modules[out].states[module_name] = 'low'
                
    return {**modules, **unfound_modules}

modules = process_input(input_20)

The first part of the puzzle asks to find the number of low and high pulses transmitted between the modules, when the button is pressed $1000$ times. Here are a couple of helper function, that allow us to track these:

reset_modules = used to reset the modules to their initial states (flip-flops back to Off, conjunctions back to ‘low’ for all source modules)
send_n_pulses = transmits $n$ low pulses to the broadcaster module, and counts the total number of low and high pulses subsequently transmitted. Each time, a low pulse is transmitted to the broadcaster module, and all subsequent pulses are sent and resolved before the next press of the button. To handle, this we can use a priority queue - specifically, using a deque from the standard Python module collections. When a pulse is created, it is added to the end of the priority queue; once all modules have processed a particular pulse, a new pulse can be taken from the front of the queue. In this way, all currently existing pulses are handled before any subsequently created pulses.

def reset_modules(modules):
    # Reset modules to their initial states
    for module_string in modules:
        modules[module_string].reset()

def send_n_pulses(modules, n, reset=True, print_pulses=False):
    # Hit the button n times, transmitting n low pulses
    # to the broadcaster module. Count the total number 
    # of low and high pulses transmitted
    
    # Reset all modules if necessary
    if reset:
        reset_modules(modules)
        
    n_pulses = {'low': 0, 'high': 0}
    for _ in range(n):
        
        # Use a double-ended queue to track the pulses
        pulses = deque()
        
        # Transmit pulse from button
        pulses.append(Pulse('low', 'button', 'broadcaster'))
        n_pulses['low'] += 1
        
        while len(pulses) > 0:
            # Take pulse from the front of the queue
            pulse = pulses.popleft()
            if print_pulses:
                print(pulse)

            # Process pulse and create new pulses
            # to add to end of priority queue
            module = modules[pulse.destination]
            out_pulses = module.process_pulse(pulse)
            for out_pulse in out_pulses:
                n_pulses[out_pulse.pulse_type] += 1
                pulses.append(out_pulse)
                
    return n_pulses

Let’s test this out on the provided test examples:

test_1 = [
    'broadcaster -> a, b, c',
    '%a -> b',
    '%b -> c',
    '%c -> inv',
    '&inv -> a'
]

test_1_modules = process_input(test_1)

_ = send_n_pulses(test_1_modules, 1, print_pulses=True)

button -low-> broadcaster
broadcaster -low-> a
broadcaster -low-> b
broadcaster -low-> c
a -high-> b
b -high-> c
c -high-> inv
inv -low-> a
a -low-> b
b -low-> c
c -low-> inv
inv -high-> a

This matches the expected sequence of pulses for this first example. For the second example, a sequence of 4 button presses completes a cycle:

test_2 = [
    'broadcaster -> a',
    '%a -> inv, con',
    '&inv -> b',
    '%b -> con',
    '&con -> output'
]

test_2_modules = process_input(test_2)

for i in range(4):
    print(f'\n====== Press {i+1} ======\n')
    send_n_pulses(test_2_modules, 1, reset=False, print_pulses=True)

====== Press 1 ======

button -low-> broadcaster
broadcaster -low-> a
a -high-> inv
a -high-> con
inv -low-> b
con -high-> output
b -high-> con
con -low-> output

====== Press 2 ======

button -low-> broadcaster
broadcaster -low-> a
a -low-> inv
a -low-> con
inv -high-> b
con -high-> output

====== Press 3 ======

button -low-> broadcaster
broadcaster -low-> a
a -high-> inv
a -high-> con
inv -low-> b
con -low-> output
b -low-> con
con -high-> output

====== Press 4 ======

button -low-> broadcaster
broadcaster -low-> a
a -low-> inv
a -low-> con
inv -high-> b
con -high-> output

Finally, we can press the button for the full set of modules $1000$ times and count the number of pulses; the final answer to submit is the product of the numbers of low and high pulses:

n_pulses = send_n_pulses(modules, 1000)
n_pulses['low']*n_pulses['high']

730797576

So the answer to part 1 is: 730797576.

Part 2

In part 2 of this puzzle, we are asked to find the minimum number of button presses required to send a low pulse to the rx module. After closer examination of the structure of the various modules (see the page at the end of this post!), we can identify the purpose of each of them; the clusters dict splits the modules up into various functional groups, and the visualization using graphviz helps to demonstrate what is going on:

# Group the modules into different clusters
clusters = {
    'chain_1': ['hx', 'xq', 'rm', 'tp', 'kh', 'qc', 'xh', 'vm', 'jm', 'cq', 'tg', 'fb'],
    'chain_2': ['kb', 'cv', 'vx', 'pt', 'qq', 'rz', 'tz', 'kn', 'gg', 'cp', 'rd', 'xk'],
    'chain_3': ['nj', 'kp', 'xx', 'vp', 'sj', 'mt', 'mx', 'rv', 'rr', 'bq', 'xb', 'gr'],
    'chain_4': ['xr', 'qv', 'gx', 'vh', 'qn', 'lz', 'xv', 'zk', 'lv', 'mj', 'hb', 'vj'],
    'rx_cluster': ['rx', 'gh', 'rk', 'cd', 'zf', 'qx']
}
rest = ['broadcaster', 'xz', 'jj', 'bz', 'gf']

# Plot the modules to visualize the structure
from graphviz import Digraph
fontsize='30'
g = Digraph('G', filename='day20.gv', format='png')

for name, module in modules.items():
    for conn in module.connected:
        for cluster_name, cluster in clusters.items():
            if name in cluster and conn in cluster:
                with g.subgraph(name=f'cluster_{cluster_name}') as c:
                    c.edges([(name, conn)]) 
        if name in rest or conn in rest:
            g.edge(name, conn)
            
    if isinstance(module, FlipFlop):
        g.node(name, style='filled', color='lightblue', fontsize=fontsize, group='flipflop')
    if isinstance(module, Conjunction):
        g.node(name, style='filled', color='orange', fontsize=fontsize)
    if isinstance(module, Broadcaster):
        g.node(name, style='filled', color='pink', fontsize=fontsize)
    if isinstance(module, UntypedModule):
        g.node(name, style='filled', color='yellow', fontsize=fontsize)
    
    for cluster_name in clusters:
        with g.subgraph(name=f'cluster_{cluster_name}') as c:
            c.attr(peripheries='0')
        
g.view()


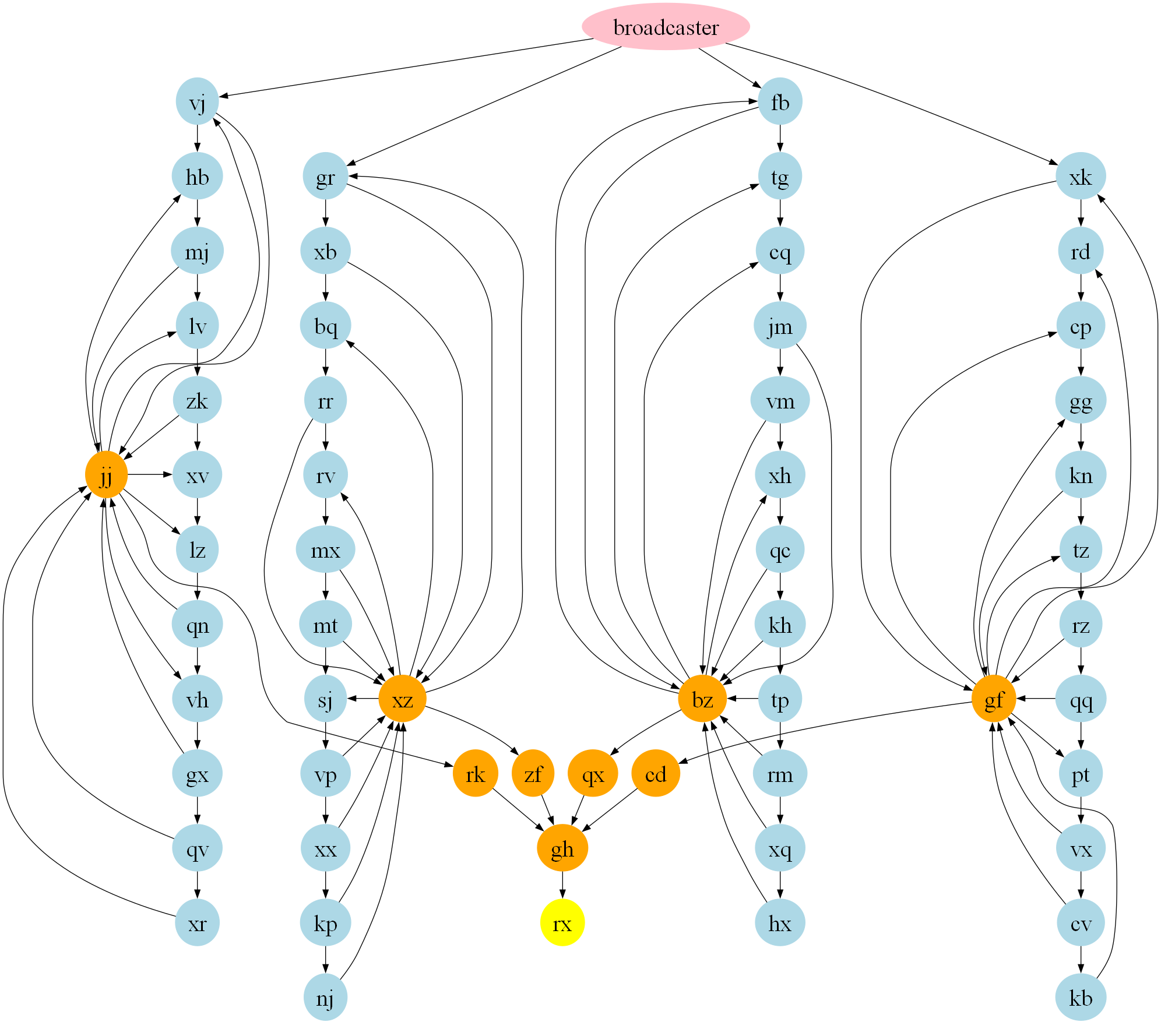Diagram visualizing the structure of the modules. The `FlipFlop` modules are in blue, `Conjunction` modules in orange, `Broadcaster` module in pink, and the final output module `nx` is in yellow.

Let’s break down what is going on here:

The different types of modules are colour coded:
- FlipFlop = blue
- Conjunction = orange
- Broadcaster = pink
- UntypedModule = yellow
The rx module is the only UntypedModule. It only receives pulses from the gh module, which is a Conjunction module. This means that a low pulse will only be sent to rx when all the inputs to gh are ‘high’.
There are 4 modules which gh receives pulses from: rk, cd, zf and qx. Each of these are Conjunction modules, with a single input module (jj, gf, xz and bz respectively). A Conjunction module with a single input effectively acts as a NOT gate, switching low pulses for high pulses (and vice versa). Therefore, gh transmits a low pulse only when each of jj, gf, xz and bz have sent low pulses.
There are 4 groups, each containing 12 FlipFlop modules connected in sequence. Each group has an associated Conjunction module (one of jj, gf, xz or bz), which outputs to some (but not all) of the modules in the group. Some (but not all) of the FlipFlop modules also output to the Conjunction module. Each of the FlipFlop modules is either an output of the Conjunction, or outputs to the Conjunction; the first module in the chain does both.
The only Broadcaster module, which receives the inital low pulse from the button, is connected to the first FlipFlop in each of the groups. Each time the button is pressed, this module will transmit a new low pulse to the first FlipFlop in each group.
When each chain of FlipFlop modules receives a new low pulse, it propogates along the chain, updating the on/off states of each module. The key insight is that the on/off states of the modules in the chain represent a binary number, and each low pulse increments this number by 1:

Pulse/state	Binary arithmetic
Off -> On, send high pulse	0 -> 1, no carry digit
On -> Off, send low pulse	1 -> 0, carry digit to next module
Receive low pulse	Carried 1 received
Receive high pulse	No carry received

Let’s test this by sending a few pulses into each chain, and looking at the binary number recorded on each chain:

def binary_states(modules, names):
    ret = ''
    for name in names:
        mod = modules[name]
        ret += '1' if mod.state else '0'
    return ret

reset_modules(modules)
for i in range(8):
    send_n_pulses(modules, 1, reset=False, print_pulses=False)
    print(f'======= Press {i+1} ======')
    print(binary_states(modules, clusters['chain_1']))
    print(binary_states(modules, clusters['chain_2']))
    print(binary_states(modules, clusters['chain_3']))
    print(binary_states(modules, clusters['chain_4']))

======= Press 1 ======
000000000001
000000000001
000000000001
000000000001
======= Press 2 ======
000000000010
000000000010
000000000010
000000000010
======= Press 3 ======
000000000011
000000000011
000000000011
000000000011
======= Press 4 ======
000000000100
000000000100
000000000100
000000000100
======= Press 5 ======
000000000101
000000000101
000000000101
000000000101
======= Press 6 ======
000000000110
000000000110
000000000110
000000000110
======= Press 7 ======
000000000111
000000000111
000000000111
000000000111
======= Press 8 ======
000000001000
000000001000
000000001000
000000001000

As shown here, each press of the button increments the count on each chain by 1.

For each chain, the associated Conjunction only sends high pulses (with no effect on the FlipFlop modules), until it has received only high pulses from all of its inputs. This happens when each of the carefully chosen FlipFlop inputs have sent high pulses to it - i.e., they have all just been switched on.

The first time that all of these modules are switched on simultaneously is when the incremental counter has reached the binary number with $1$s in these positions, and $0$s everywhere else. In other words, by recording the binary number defined by the chain, we find the number of button presses required to activate the Conjunction for the first time. Reading these numbers off the diagram for each chain:

print(int('111011010001', 2))
print(int('111101101011', 2))
print(int('111111011001', 2))
print(int('111010010101', 2))

Once one of these numbers is hit, a low pulse is sent from the Conjunction to all of the FlipFlop modules in the chain that did not activate the Conjunction, as well as the first in the chain. This will turn all of the off states ($0$s) in the chain to on states ($1$s), thereby sending the counter to its maximum value; then, the final pulse to the start of the chain makes the counter overflow, taking it back to $0$.

We can verify this by taking a look at the incremental counters, near one of these numbers:

reset_modules(modules)
send_n_pulses(modules, 3730, reset=False, print_pulses=False)
for i in range(5):
    send_n_pulses(modules, 1, reset=False, print_pulses=False)
    print(f'======= Press {i+1} ======')
    print(binary_states(modules, clusters['chain_1']))
    print(binary_states(modules, clusters['chain_2']))
    print(binary_states(modules, clusters['chain_3']))
    print(binary_states(modules, clusters['chain_4']))

======= Press 1 ======
111010010011
111010010011
111010010011
111010010011
======= Press 2 ======
111010010100
111010010100
111010010100
111010010100
======= Press 3 ======
111010010101
111010010101
111010010101
000000000000
======= Press 4 ======
111010010110
111010010110
111010010110
000000000001
======= Press 5 ======
111010010111
111010010111
111010010111
000000000010

As expected, on the 3rd button press, the last of the incremental counters is zeroed; after this, it continues to count up from zero. This happens for all of the chains, at the number obtained from the modules in the chain connected to the Conjunction (i.e. 3793, 3947, 4057 or 3733).

So when is the final rx module activated? Only when each of these intermediate Conjunction modules is activated simultaneously. This happens when each of the incremental counters is reset at the same time - i.e. when the button has been hit a multiple of all of the chain numbers (i.e. 3793, 3947, 4057 or 3733). The first time that this happens must be the lowest common multiple of these numbers:

math.lcm(4057, 3793, 3947, 3733)

226732077152351

So the answer to part 2 of the puzzle is: 226732077152351.

My working out for this puzzle:

Module diagram

❄️ Back to Advent of Code 2023 solutions homepage ❄️

Share on

Twitter Facebook LinkedIn

Michael Cole

Advent of Code 2023, Day 20

Part 1

Part 2

My working out for this puzzle:

Share on

Comments

You May Also Enjoy

How to play one player 501

How can I reach checkout before my opponent?

How do I throw high scoring darts?

The Quadro board - why did it flop?